Question

For fixed-rate bonds it's important to realize that the value of the bond has a(n)-Select relationship to the level of interest rates. If interest rates rise, then the value of the bond-select- however, if interest rates fall, then the value of the bond-select- ▼ -A-Select- ▼ | bond is one that sells below its par value. This situation occurs whenever the going rate of interest is above the coupon rate. Over time its value will -Select-approaching its maturity value at maturity. A -Select-bond is one that sells above its par value. This situation occurs whenever the going rate of interest is below the coupon rate. Over time its value will -Select- approaching its maturity value at maturity. A par value bond is one that sells at par; the bond's coupon rate is equal to the going rate of interest. Normally, the coupon rate is set at the going market rate the day a bond is issued so it sells at par initially Quantitative Problem: Potter Industries has a bond issue outstanding with an annual coupon of 6% and a 10-year maturity. The par value of the bond is $1,000. If the going annual interest rate is 7%, what is the value of the bond? Round your answer to the nearest cent. Do not round intermediate calculations Quantitative Problem: Potter Industries has a bond issue outstanding with a 6% coupon rate with semiannual payments of $30, and a 10-year maturity. The par value of the bond is $1,000. If the going annual interest rate is 796, what is the value of the bond? Round your answer to the nearest cent. Do not round intermediate calculations.

Answer 1

Answer is explained in the explanation section below.

Step-by-step explanation:

It's necessary to remember that the value of fixed-rate bonds is inversely proportional to the level of interest rates. The value of the bond decreases as interest rates rise; moreover, the value of the bond rises as interest rates fall. A Bond with a lower coupon sells for less than its face value. When the going rate of interest is higher than the coupon rate, this condition arises. The value of the asset would increase over time. A higher coupon bond is one that sells for a higher price than its face value. When the going rate of interest is lower than the coupon rate, this condition arises. Its value will gradually decrease until it reaches its maturity value. A par value bond that sells at par, with a coupon rate equal to the current interest rate. The coupon is usually set at the going market rate on the day the bond is sold, so it sells at par at first.

Calculations:

C = Coupon Payments = $60 (Par Value x Coupon Rate)

n = number of years = 10

i = market rate or required yield = 7% = 0.007

K = number of coupon payments in 1 year = 1

P = value at maturity or par value = 1000

Present value of ordinary annuity formula:

Bond Price = C/k *
`[(1 - (1)/((1 + (i)/(k))^(nk) ) )/((i)/(k) ) ]` +
`(P)/((1 + (i)/(k))^(nk) )`

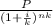
Just plug in the values and you will get:

Bond Price = 60 x 7.02 + 508.35

Bond Price = 421.41 508.35

Bond Price = $929.76

Similarly,

Data:

C = Coupon Payments = $60 (Par Value x Coupon Rate)

n = number of years = 10

i = market rate or required yield = 7% = 0.007

K = number of coupon payments in 1 year = 2

P = value at maturity or par value = 1000

Present value of ordinary annuity formula:

Bond Price = C/k *
`[(1 - (1)/((1 + (i)/(k))^(nk) ) )/((i)/(k) ) ]` +
`(P)/((1 + (i)/(k))^(nk) )`

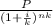
Just plug in the values and you will get:

Bond Price = 30 x 14.21 + 502.57

Bond Price = 426.37 + 502.57

Bond Price = $928.94