Solution :
The motion in the y direction.
The time taken by the toy rocket to hit the ground,
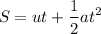
S = distance travelled = 30 m
u = 0 m/s
a =
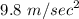
t= time in seconds
Therefore,
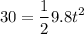
t = 2.47 sec
Now motion in the x direction,
u = 12 m/sec
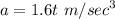
Upon integration 'v' with respect to 't'
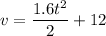
Once again integrating with respect to t,
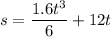

= 0.0176+29.64
= 29.65 m
Therefore, the toy rocket will hit the ground at 29.65 m from the building.