Answer:
a) the acceleration of the particle is ( v
 ² - v
² - v
 ² ) / 2as
² ) / 2as
b) the integral W =
 m(
m(
 ² - v
² - v
 ² )
² )
Step-by-step explanation:
Given the data in the question;
force on particle F = ma
displacement s = x
 - x
- x

work done on the particle W = Fs = mas
we know that; change in energy = work done { work energy theorem }
 m( v
m( v
 ² - v
² - v
 ² ) = mas
² ) = mas
 ( v
( v
 ² - v
² - v
 ² ) = as
² ) = as
( v
 ² - v
² - v
 ² ) = 2as
² ) = 2as
a = ( v
 ² - v
² - v
 ² ) / 2as
² ) / 2as
Therefore, the acceleration of the particle is ( v
 ² - v
² - v
 ² ) / 2as
² ) / 2as
b) Evaluate the integral W =
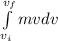
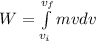
![W =m[(v^(2) )/(2) ]^(vf)_(vi)](https://img.qammunity.org/2022/formulas/physics/college/7dr48oba3ddsbylntl6wwoigd4593un1yu.png)
W =
 m(
m(
 ² - v
² - v
 ² )
² )
Therefore, the integral W =
 m(
m(
 ² - v
² - v
 ² )
² )