Answer:
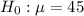 and
and
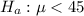
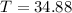
The null hypothesis is not rejected
Explanation:
Given
Random sample of 50 commuter times
Solving (a): The null and alternate hypothesis
From the question, a previous census shows that:
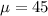 and
and
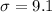
This is the null hypothesis i.e.
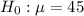
Reading further, a new test was to show whether the average has decreased.
This is the alternate hypothesis, and it is represented as:
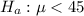
Solving (b) and (c): The test statistic (T).
This is calculated using:
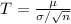
In this case:

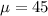 and
and
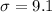
So:
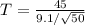
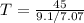
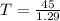
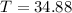
Solving (c): Accept or reject null hypothesis
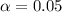
First calculate the degrees of freedom (df)
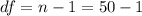
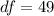
From the t distribution table,
At:
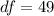 ,
,
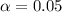 and
and
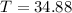
the t score is:
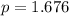
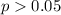
So, the null hypothesis is not rejected