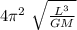Question

Exact solutions for gravitational problems involving more than two bodies are notoriously difficult. One solvable problem involves a configuration of three equal-mass objects spaced in an equilateral triangle. Forces due to their mutual gravitation cause the configuration to rotate. Suppose three identical stars, each of mass M, form a triangle of side L. Find an expression for the period of their orbital motion.

Answer 1

T =
`4\pi ^2 \ \sqrt{ (L^3)/(GM) }`

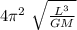
Step-by-step explanation:

Let's analyze the situation, as the stars have the same mass and all are at the same distance, the magnitude of the force is constant, even when its direction changes, Let's use Newton's second law

F = m a

in this case the force is the universal attraction

F = G M₁ M₂ / r²

they relate it is centripetal

a = v² / r = w² r

we substitute

G M² / r² = M w² r

w² =
`(G M)/(r^3)`

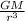
angular velocity is related to frequency and period

w = 2π f = 2π / T

we substitute

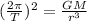
`((2\pi )/(T ))^2 = (G M)/(r^3)`

T =
`4\pi^2 \ \sqrt{ (r^3)/(G M)}`

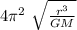
in this case r= L

T =
`4\pi ^2 \ \sqrt{ (L^3)/(GM) }`