Answer:
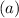
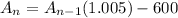 where
where
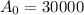
(b) Above $150
Step-by-step explanation:
Given
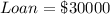
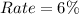 --- annually
--- annually
Solving (a): Recursion for the amount at the end of n month
The base case is:
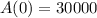
Next, we calculate the monthly rate (r)
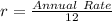
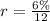
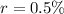
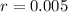
The loan amount remaining at the end of month n is then calculated as:
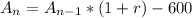 ---[The 600 represents the monthly payment]
---[The 600 represents the monthly payment]
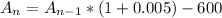
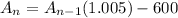
Solving (b):
Suppose the borrower requests for a lower monthly payment, then the following condition will exist:
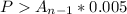
i.e. the monthly payment will exceed the monthly interest
Let
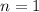
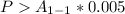
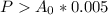
Substitute 30000 for
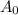
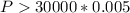
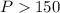
His monthly payment must exceed $150