Answer:
![l = \sqrt[3]{(2V)/(7)}](https://img.qammunity.org/2022/formulas/mathematics/college/vjm8se4hz6tch3p3lyo3f0bwgona9f0w31.png)
![b = \sqrt[3]{(2V)/(7)}](https://img.qammunity.org/2022/formulas/mathematics/college/k0zjpnup3lr3v6o5hhnldwshtyv54ttg07.png)
![h = \sqrt[3]{(49V)/(4)}](https://img.qammunity.org/2022/formulas/mathematics/college/gq4f0nst5x9yeadkallm7q7fqdqsrhcjao.png)
Explanation:
Represent the volume of the box with V and the dimensions with l, b and h.
The volume (V) is:
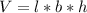
Make h the subject of the formula
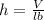
The surface area (S) of the aquarium is:
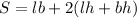
Where lb represents the area of the base (i.e. slate):
The cost (C) of the surface area is:
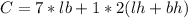
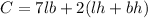
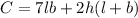
Substitute
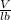 for h in the above equation
for h in the above equation
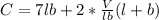
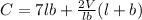
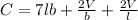
Differentiate with respect to l and with respect to b
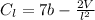
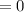
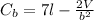
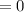
To solve for b and l, we equate both equations and set l to b (to minimize the cost)
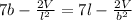
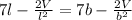
By comparison:
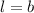
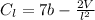
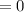 becomes
becomes
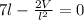
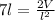
Cross Multiply
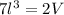
Solve for l
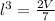
![l = \sqrt[3]{(2V)/(7)}](https://img.qammunity.org/2022/formulas/mathematics/college/vjm8se4hz6tch3p3lyo3f0bwgona9f0w31.png)
Recall that:
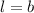
![b = \sqrt[3]{(2V)/(7)}](https://img.qammunity.org/2022/formulas/mathematics/college/k0zjpnup3lr3v6o5hhnldwshtyv54ttg07.png)
Also recall that:
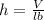
![h = \frac{V}{\sqrt[3]{(2V)/(7)}*\sqrt[3]{(2V)/(7)}}](https://img.qammunity.org/2022/formulas/mathematics/college/u7zmtewxs54zt8e87acrc2f5tq6dtx1ld4.png)
![h = \frac{V}{\sqrt[3]{(4V^2)/(49)}}](https://img.qammunity.org/2022/formulas/mathematics/college/un5mdmoccruq9ceka5t7s7uvibvgl8dex8.png)
Apply law of indices
![h = \sqrt[3]{(49V^3)/(4V^2)}](https://img.qammunity.org/2022/formulas/mathematics/college/3d0cr8bw6atr9gz3935cii0zycw8f8nxvo.png)
![h = \sqrt[3]{(49V)/(4)}](https://img.qammunity.org/2022/formulas/mathematics/college/gq4f0nst5x9yeadkallm7q7fqdqsrhcjao.png)
The dimension that minimizes the cost of material of the aquarium is:
![l = \sqrt[3]{(2V)/(7)}](https://img.qammunity.org/2022/formulas/mathematics/college/vjm8se4hz6tch3p3lyo3f0bwgona9f0w31.png)
![b = \sqrt[3]{(2V)/(7)}](https://img.qammunity.org/2022/formulas/mathematics/college/k0zjpnup3lr3v6o5hhnldwshtyv54ttg07.png)
![h = \sqrt[3]{(49V)/(4)}](https://img.qammunity.org/2022/formulas/mathematics/college/gq4f0nst5x9yeadkallm7q7fqdqsrhcjao.png)