Question

Two bicycle tires are set rolling with the same initial speed of 4.0 m/s along a long, straight road, and the distance each travels before its speed is reduced by half is measured. One tire is inflated to a pressure of 40 psi and goes a distance of 18.2 m; the other is at 105 psi and goes a distance of 92.6 m. Assume that the net horizontal force is due to rolling friction only and take the free-fall acceleration to be g = 9.80 m/s2. What is the coefficient of rolling friction μr for the tire under low pressure?

Answer 1

The coefficient of rolling friction will be "0.011".

Step-by-step explanation:

The given values are:

Initial speed,

`v_i = 4.0 \ m/s`

then,

`v_f=(4.0)/(2)`

`=2.0 \ m/s`

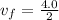
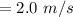
Distance,

s = 18.2 m

The acceleration of a bicycle will be:

⇒
`a=(v_f^2-v_i^2)/(2s)`

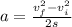
On substituting the given values, we get

⇒
`=((2.0)^2-(4.0)^2)/(2* 18.2)`

⇒
`=(4-8)/(37)`

⇒
`=(-4)/(37)`

⇒
`=0.108 \ m/s^2`

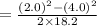
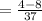
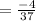
As we know,

⇒
`f=ma`

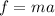
and,

⇒
`\mu_rmg=ma`

⇒
`\mu_r=(a)/(g)`

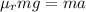
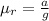
On substituting the values, we get

⇒
`=(0.108)/(9.8)`

⇒
`=0.011`