1 Answer

Justik · Answer 1 · 2022-08-07T01:12:25+0000

Answer: There is no polygon with the sum of the measures of the interior angles of a polygon is 1920°.

Explanation:

The sum of the measures of interior angles of a polygon with
sides is given by:-

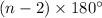
$(n-2)*180^(\circ)$

Given: The sum of the measures of the interior angles of a polygon is 1920°.

i.e.
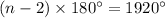
$(n-2)*180^(\circ)=1920^(\circ)$

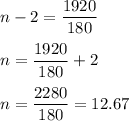
$n-2=(1920)/(180)\\\\ n= (1920)/(180)+2\\\\ n=(2280)/(180)=12.67$

But number of sides cannot be in decimal.

Hence, there is no polygon with the sum of the measures of the interior angles of a polygon is 1920°.

Please log in or register to add a comment.