Question

During the first 13 weeks of the television season, the Saturday evening 8:00 P.M. to 9:00 P.M. audience proportions were recorded as ABC 29%, CBS 28%, NBC 25%, and independents 18%. A sample of 300 homes two weeks after a Saturday night schedule revision yielded the following viewing audience data: ABC 95 homes, CBS 65 homes, NBC 87 homes, and independents 53 homes. Test with = .05 to determine whether the viewing audience proportions changed.

Required:
Compute the value of the 2 test statistic (to 2 decimals). The p value is Has a significant change occurred in viewing audience proportions?

Answer 1

- The value of the 2 test statistic is 6.98

- There is no sufficient evidence to reject the claim of the specific distribution

Explanation:

Given

Proportion (p)

`ABC = 29\% = 0.29\\CBS = 28\% = 0.28\\NBC = 25\% = 0.25\\Others = 18\% = 0.18\\`

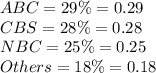
Samples

`ABC = 95\\CBD = 65\\NBC = 87\\Others = 53\\\alpha = 0.05`

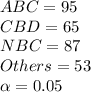
First, we formulate a table for chi square totals:

`x^2 = ((O - E)^2)/(E)`

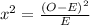
Where

O = Observed Frequency and E = Expected Frequency

So, we have:

`\begin{array}{cccccc}{\ } & {O} & {E = np} & {O - E} & {(O -E)^2} & {x^2 = ((O - E)^2)/(E)} \ \\ \\ {0.29} & {95} & {87} & {8} & {64} & {0.736} &{0.28} & {65} & {84} & {-19} & {361} & {4.300} & {0.25} & {87} & {75} & {12} & {144} & {1.920} & {0.18} & {53} & {54} & {-1} & {1} & {0.019}\ \end{array}`

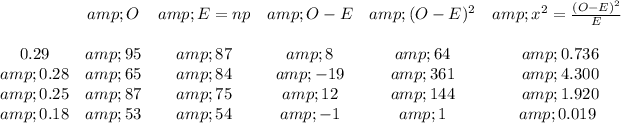
For ABC

`E = np = 300 * 0.29= 87`

`O-E =95 - 87 = 8`

`(O-E)^2 = 8^2 = 64`

`x^2 = ((O - E)^2)/(E) = (64)/(87) = 0.736`

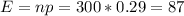
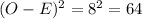
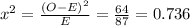
For CBS

`E =np = 300 * 0.28 = 84`

`O -E = 65 - 84 = -19`

`(O -E)^2 = (-19)^2 = 361`

`x^2 = ((O - E)^2)/(E) = (361)/(84) = 4.300`

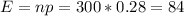
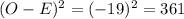
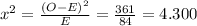
For NBC

`E =np = 300 * 0.25 = 75`

`O -E = 87 - 75 = 12`

`(O -E)^2 = (12)^2 = 144`

`x^2 = ((O - E)^2)/(E) = (144)/(75) = 1.920`

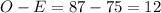
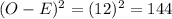
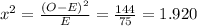
For others:

`E = np = 300 * 0.18 =54`

`O - E = 53 - 54 = -1`

`(O - E)^2 = (-1)^2= 1`

`x^2 = ((O - E)^2)/(E) = (1)/(54) = 0.019`

`\sum x^2 = 0.736 + 4.300 + 1.920 + 0.019`

`\sum x^2 = 6.975`

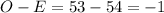
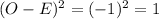
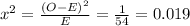
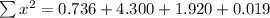
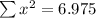
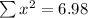`\sum x^2 = 6.98` --- approximated

The value of the 2 test statistic is 6.98

Next, is to determine the p value:

Calculate the degree of freedom

`df = n - 1`

`df = 4 - 1`

`df = 3`

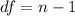
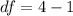
Using the
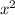`x^2` table in the 3rd row,

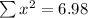`\sum x^2 = 6.98` corresponds to:

`p = 0.072699`

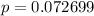
The value of p is:

`0.05 < P < 0.10`

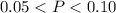
This implies that, we fail to reject H o