Question

Use sigma notation to represent the sum of a geometric series with a first term of 3 and a common ratio of . A. B. C. D.

Answer 1

`\Sigma_(k=1)^(n)[3((10)/(9) )^(k-1)]`

Explanation:

A geometric sequence is a list of numbers having a common ratio. Each term after the first is gotten by multiplying the previous one by the common ratio.

The first term is denoted by a and the common ratio is denoted by r.

A geometric sequence has the form:

a, ar, ar², ar³, . . .

The nth term of a geometric sequence is
`ar^(n-1)`

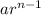
Therefore the sum of the first n terms is:

`\Sigma_(k=1)^(n)(ar^(k-1))`

Given a geometric series with a first term of 3 and a common ratio of 10/9, the sum of the first n terms is:

`\Sigma_(k=1)^(n)[3((10)/(9) )^(k-1)]`