Question

Determine if the following statements are true or false. If true give a reason or cite a theorem and if false, give a counter example.

a. If {a _n} is bounded, then it converges.
b. If {a _n} is not bounded, then it diverges.
c. If {a _n} diverges, then it is not bounded

Give an example of divergent sequences {a _n} and {b _n} such that {a _n + b _n} converges

Answer 1

a. False the series
`\sum\limits_(i=1)^\infty (-1)^n`is bounded but does not converge

b. False, xₙ = n + (-1)ⁿ⁻¹(n - 1) does not diverge to infinity but it is not bounded for n ≥ 1

c. False some bounded sequences are divergent

An example of divergent sequences, aₙ, and bₙ, such that aₙ + bₙ converges is
`a_n = \sum\limits_(n) (1)/(n) , \, b_n = \sum\limits_(n) (-1)/(n)`

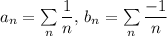
`\sum\limits_(n) (1)/(n) + \sum\limits_(n) (-1)/(n)` is convergent

Explanation: