Answer:
The 95% confidence interval for the true difference in the proportion of tomato plants like these that would experience damage after receiving the kelp treatment and no kelp treatment is -0.2690 <
 < 0.02901
< 0.02901
Explanation:
The given data are;
The number of the group 1 plants that exhibited damage = 12
The number of plants in group 1, n₁ = 50
The number of the group 2 plants that exhibited damage = 18
The number of plants in group 2, n₂ = 50
The proportion of group 1 plants that exhibited damage,
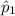 = 12/50 = 0.24
= 12/50 = 0.24
The proportion of group 2 plants that exhibited damage,
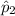 = 18/50 = 0.36
= 18/50 = 0.36
The z-value at 95% = 1.64
The confidence interval is given by the following formula;
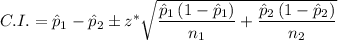
Plugging in the values, we get;
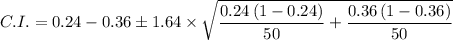
Therefore, C.I. = -0.2690 <
 < 0.02901
< 0.02901