Question

Past evidence shows that when a customer complains of an out-of-orderphone there is an 8% chance that the problem is with the inside wiring. During a 1-month period,100 complains are lodged. Assume that there have been no wide-scale problems that could beexpected to affect many phones at once, and that, for this reason, these failures are consideredto be independent.

Required:
a. Find the expected number of failures due to a problem with the inside wiring.
b. Find the probability that at least 10 failures are due to a problem with the inside wiring.
c. Would it be unusual if at most 5 were due to problems with the inside wiring? Explain, based on the probability of this occurring.

Answer 1

a. The expected number of failures due to a problem with inside wiring is 8 failures

b. The probability that at least 10 failures are due to inside wiring is approximately 0.176

c. It will be not unusual

Step-by-step explanation:

The probability that the problem of an out of order is the inside wiring, P(x) = 8%

The number of complaints in a month period, x = 100

a. The expected number of failures due to a problem with inside wiring, E(x) = x·P(x)

∴ E(x) = 100 × 8% = 8

The expected number of failures due to a problem with inside wiring, E(x) = 8 failures

b. The probability that at least 10, P₁₀, failures are due to inside wiring is given as follows;

The probability of success, P = 0.08, therefore, the probability of failure, q = 1 - 0.08 = 0.92

P =
`_nC_r`·
`P^r`·
`q^(n-r)`

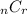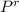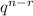
P₀ = ₁₀₀C₀·(0.08)⁰·(0.92)¹⁰⁰ = 0.000239211874657

P₁ = ₁₀₀C₁·(0.08)¹·(0.92)⁹⁹ = 0.00208010325

P₂ = ₁₀₀C₂·(0.08)²·(0.92)⁹⁸ = 0.00895348793

P₃ = ₁₀₀C₃·(0.08)³·(0.92)⁹⁷ = 0.02543309616

P₄ = ₁₀₀C₄·(0.08)⁴·(0.92)⁹⁶ = 0.0536306593

P₅ = ₁₀₀C₅·(0.08)⁵·(0.92)⁹⁵ = 0.0895398833653

P₆ = ₁₀₀C₆·(0.08)⁶·(0.92)⁹⁴ = 0.123279549561

P₇ = ₁₀₀C₃·(0.08)⁷·(0.92)⁹³ = 0.143953759735

P₈ = ₁₀₀C₈·(0.08)⁸·(0.92)⁹² = 0.145518474516

P₉ = ₁₀₀C₉·(0.08)⁹·(0.92)⁹¹ = 0.129349755125

P₁₀ = ₁₀₀C₁₀·(0.08)¹⁰·(0.92)⁹⁰ = 0.10235502362

∴ P₀ + P₁ + P₂ + P₃ + P₄ + P₅ + P₆ + P₇ + P₈ + P₉ + P₁₀ = 0.82433004464

The probability of at least 10 failures are due problem with the inside wiring = 1 - (P₀ + P₁ + P₂ + P₃ + P₄ + P₅ + P₆ + P₇ + P₈ + P₉ + P₁₀) = 1 - 0.82433004464 = 0.175666995536

The probability of at least 10 failures are due problem with the inside wiring = 0.175666995536 ≈ 0.176

c. The probability of at most 5 failures are due problem with the inside wiring = P₀ + P₁ + P₂ + P₃ + P₄ + P₅ = 0.179876441908

Therefore, given that probability of at most 5 failures > The probability of 8 failures it will be not unusual since the cause of failure is more (92%) due to other causes which are more likely and therefore increase in the probability that there are fewer failures due inside wiring