Answer:
The amount of thermal energy needed is 15167500 joules.
Step-by-step explanation:
By First Law of Thermodynamics, we see that amount of thermal energy (
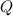 ), in joules, is equal to the change in internal energy. From statement we understand that change in internal energy consisting in two latent components (
), in joules, is equal to the change in internal energy. From statement we understand that change in internal energy consisting in two latent components (
 ,
,
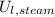 ), in joules, and two sensible component (
), in joules, and two sensible component (
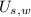 ), in joules, that is:
), in joules, that is:
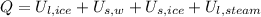 (1)
(1)
By definitions of Sensible and Latent Heat, we expanded the formula:
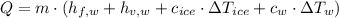 (2)
(2)
Where:
 - Mass, in kilograms.
- Mass, in kilograms.
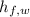 - Latent heat of fussion of water, in joules per kilogram.
- Latent heat of fussion of water, in joules per kilogram.
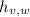 - Latent heat of vaporization of water, in joules per kilogram.
- Latent heat of vaporization of water, in joules per kilogram.
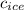 - Specific heat of ice, in joules per kilogram per degree Celsius.
- Specific heat of ice, in joules per kilogram per degree Celsius.
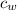 - Specific heat of water, in joules per kilogram per degree Celsius.
- Specific heat of water, in joules per kilogram per degree Celsius.
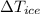 - Change in temperature of ice, measured in degrees Celsius.
- Change in temperature of ice, measured in degrees Celsius.
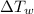 - Change in temperature of water, measured in degrees Celsius.
- Change in temperature of water, measured in degrees Celsius.
If we know that
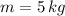 ,
,
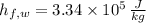 ,
,
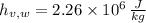 ,
,
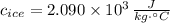 ,
,
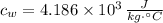 ,
,
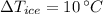 and
and
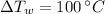 , then the amount of thermal energy is:
, then the amount of thermal energy is:
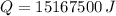
The amount of thermal energy needed is 15167500 joules.