Question

PLEASE HELPPPPP

The revenue made by a car
company from the sale of y cars is given by 0.003y! +
10y. The cost to produce y cars is given by the polynomial 20y + 1,000,000. Write
a polynomial expression for the profit from making and selling y cars. Find the
profit the company will make if it sells 30,000 cars.

Answer 1

Part A

The polynomial expression for the profit from selling and making 'y' cars is 0.003·y² - 10·y - 1,000,000

Part B

The profit made from selling 30,000 cars is 1,670,000

Explanation:

Part A

Taking the revenue, 'R', made by the car company for the sale of 'y' cars as R = 0.003·y² + 10·y

The cost to produce 'y' cars, C = 20·y + 1,000,00

The profit, 'P', from making and selling 'y' cars is given as follows;

P = R - C

∴ 0.003·y² + 10·y - (20·y + 1,000,00) = 0.003·y² - 10·y - 1,000,00

An expression of the polynomial for the profit 'P', from selling and making 'y' cars is therefore presented as follows;

0.003·y² - 10·y - 1,000,000

Part B

The profit made from selling 30,000 cars, (y = 30,000) is given as follows;

= 0.003·y² - 10·y - 1,000,000

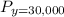`P_(y = 30,000)` = 0.003 × 30,000,000² - 10×3,000 - 1,000,000 = 1,670,000

The profit made from selling 30,000 cars = 1,670,000.