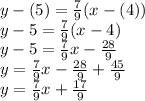Question

Write an equation of the line that passes through a pair of points:
(-5, - 2), (4, 5)

Answer 1

Answer (assuming it can be written in slope-intercept form):

`y = (7)/(9) x+(17)/(9)`

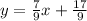
Explanation:

1) First, find the slope of the line. Use the slope formula,
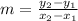`m = (y_2-y_1)/(x_2-x_1)`. Substitute the x and y values of the given points into the formula and solve:

`m = ((5)-(-2))/((4)-(-5)) \\m = (5+2)/(4+5) \\m = (7)/(9)`

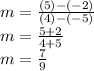
So, the slope is
`(7)/(9)`.

2) Now, use the point-slope formula
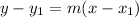`y-y_1 = m (x-x_1)` to write the equation of the line. Substitute
`m`,
`x_1`, and
`y_1` for real values.

Since
`m` represents the slope, substitute
`(7)/(9)` for it. Since
`x_1` and
`y_1` represent the x and y values of one point the line intersects, choose from any one of the given points (it doesn't matter which one, either way the result equals the same thing) and substitute its x and y values into the formula as well. (I chose (4,5), as seen below.) From there, isolate y to place the equation in slope-intercept form (
`y = mx + b` format) and find the following answer:

`y-(5) = (7)/(9) (x-(4))\\y-5 = (7)/(9) (x-4)\\y -5=(7)/(9) x-(28)/(9)\\y = (7)/(9) x-(28)/(9) +(45)/(9)\\y = (7)/(9) x+(17)/(9)`