Answer:
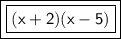
Explanation:
To factor by grouping, first divide the polynomial into 2 groups with parentheses.
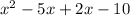
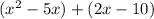
Factor the greatest common factor (GCF) out of both binomials.
For the first binomial, the GCF is x.
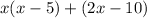
For the second binomial, the GCF is 2.
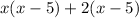
Factor out the common binomial which is (x-5).
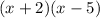
The factorized form of x²-5x+2x-10 is (x+2)(x-5)