Answer:
The first three terms of the geometry sequence would be
 ,
,
 , and
, and
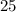 .
.
The sum of the first seven terms of the geometric sequence would be
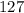 .
.
Explanation:
1.
Let
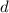 denote the common difference of the arithmetic sequence.
denote the common difference of the arithmetic sequence.
Let
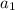 denote the first term of the arithmetic sequence. The expression for the
denote the first term of the arithmetic sequence. The expression for the
 th term of this sequence (where
th term of this sequence (where
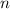 is a positive whole number) would be
is a positive whole number) would be
 .
.
The question states that the first term of this arithmetic sequence is
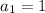 . Hence:
. Hence:
- The third term of this arithmetic sequence would be
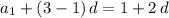 .
. - The thirteenth term of would be
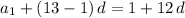 .
.
The common ratio of a geometric sequence is ratio between consecutive terms of that sequence. Let
 denote the ratio of the geometric sequence in this question.
denote the ratio of the geometric sequence in this question.
Ratio between the second term and the first term of the geometric sequence:
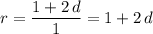 .
.
Ratio between the third term and the second term of the geometric sequence:
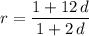 .
.
Both
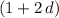 and
and
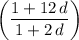 are expressions for
are expressions for
 , the common ratio of this geometric sequence. Hence, equate these two expressions and solve for
, the common ratio of this geometric sequence. Hence, equate these two expressions and solve for
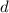 , the common difference of this arithmetic sequence.
, the common difference of this arithmetic sequence.
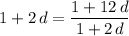 .
.
 .
.
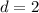 .
.
Hence, the first term, the third term, and the thirteenth term of the arithmetic sequence would be
 ,
,
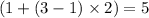 , and
, and
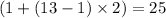 , respectively.
, respectively.
These three terms (
 ,
,
 , and
, and
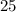 , respectively) would correspond to the first three terms of the geometric sequence. Hence, the common ratio of this geometric sequence would be
, respectively) would correspond to the first three terms of the geometric sequence. Hence, the common ratio of this geometric sequence would be
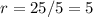 .
.
2.
Let
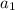 and
and
 denote the first term and the common ratio of a geometric sequence. The sum of the first
denote the first term and the common ratio of a geometric sequence. The sum of the first
 terms would be:
terms would be:
 .
.
For the geometric sequence in this question,
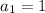 and
and
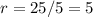 .
.
Hence, the sum of the first
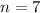 terms of this geometric sequence would be:
terms of this geometric sequence would be:
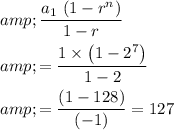 .
.