Question

Justin took a quiz with five multiple choice (A-D) and five true/false questions. How many different ways can he answer the questions?

Answer 1

Justin can answer the quiz in 32,768 different ways by considering 4^5 ways to answer the multiple choice questions and 2^5 ways for the true/false questions, and then multiplying these two possibilities.

Step-by-step explanation:

How Many Different Ways Can Justin Answer the Questions?

Justin took a quiz with five multiple choice (A-D) and five true/false questions. To calculate the number of different ways he can answer the quiz, we consider each question separately.

For every multiple choice question, there are 4 possible answers (A, B, C, or D). So for all five multiple choice questions, there are 4^5 ways Justin can answer them (1024 ways).

On the other hand, for each true/false question, there are 2 possible answers (True or False). Therefore, for all five true/false questions, there are 2^5 ways to answer them (32 ways).

To find the total number of different combinations for the entire quiz, we multiply the possibilities for both types of questions:

`4^5 * 2^5 = 1024 * 32 = 32768 \ different \ ways`

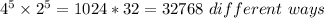
Thus, Justin can answer the quiz in 32768 different ways.

Answer 2

32,768 ways

Step-by-step explanation:

True/ false questions = 5 ; number of options = 2 (True or false)

Ways of answering = 2^5 = (2 * 2 * 2 * 2 * 2) = 32

Number of Multiple choice questions = 5

Number of options (A - D) = 4 options

Ways of answering = 4^5 = (4 * 4 * 4 * 4 * 4) = 1024

32 * 1024 = 32,768 ways