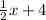Question

Here's a graph of a linear function. Write the equation that describes that function. 8 Express it in slope intercept form. Enter the correct answer. ​

Answer 1

f(x) =
`(1)/(2)x+4`

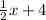
Explanation:

Let the equation of the function is,

f(x) = mx + b

Here, m = slope of the line

b = y-intercept

From the graph attached,

y-intercept 'b' = 4

Slope =
`\frac{\text{Rise}}{\text{Run}}`

=
`(4)/(8)`

=
`(1)/(2)`

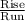
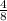
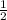
Therefore, equation of the function representing the graph will be,

f(x) =
`(1)/(2)x+4`