Answer:
See Below.
Explanation:
The first three terms of an A.P is equivalent to the first three terms of a G.P.
We want to show that this is only possible if r = 1 and d = 0.
If a is the initial term and d is the common difference, the A.P. will be:
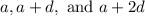
Likewise, for the G.P., if a is the initial term (and it does not equal 0) and r is the common ratio, then our sequence is:
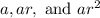
The second and third terms must be equivalent. Thus:
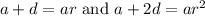
We can cancel the d. Multiply the first equation by -2:
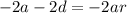
We can now add this to the second equation:
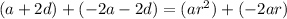
Simplify:
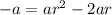
Now, we can divide both sides by a (we can do this since a is not 0):
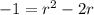
So:
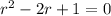
Factor:
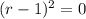
Thus:
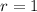
The first equation tells us that:
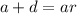
Therefore:
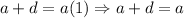
Hence:
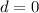
Q.E.D.