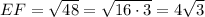Answer:
Explanation:
In rectangle ABCD, AB = 6, BC = 8, and DE = DF.
ΔDEF is one-fourth the area of rectangle ABCD.
We want to determine the length of EF.
First, we can find the area of the rectangle. Since the length AB and width BC measures 6 by 8, the area of the rectangle is:
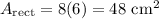
The area of the triangle is 1/4 of this. Therefore:
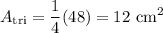
The area of a triangle is half of its base times its height. The base and height of the triangle is DE and DF. Therefore:
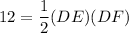
Since DE = DF:
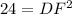
Thus:
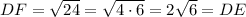
Since ABCD is a rectangle, ∠D is a right angle. Then by the Pythagorean Theorem:
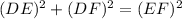
Therefore:
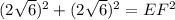
Square:
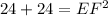
Add:
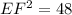
And finally, we can take the square root of both sides: