Question

The velocity, v(t), of a particle, in inches per second, at time t seconds is v(t) = 4t3 + 3t2 + 2t + 1. What distance does the particle travel over the interval 0 ≤ t ≤ 1?

Answer 1

The particle traveled 4 inches over the interval.

Explanation:

What distance does the particle travel over the interval 0 ≤ t ≤ 1?

The distance is the integral of the velocity.

So

`d(t) = \int_(0)^(1) v(t) dt`

`d(t) = \int_(0)^(1) 4t^3 + 3t^2 + 2t + 1 dt`

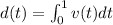
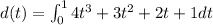
We have that:

`\int t^n dn = (t^(n+1))/(n+1)`

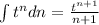
So

`d(t) = t^4 + t^3 + t^2 + t|_(0)^(1)`

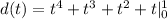
Which is:

`d(1) - d(0) = 1 + 1 + 1 + 1 = 4`

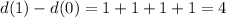
The particle traveled 4 inches over the interval.