Answer:
Approximately
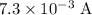 (approximately
(approximately
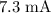 ) assuming that the magnetic field and the wire are both horizontal.
) assuming that the magnetic field and the wire are both horizontal.
Step-by-step explanation:
Let
 denote the angle between the wire and the magnetic field.
denote the angle between the wire and the magnetic field.
Let
 denote the magnitude of the magnetic field.
denote the magnitude of the magnetic field.
Let
 denote the length of the wire.
denote the length of the wire.
Let
 denote the current in this wire.
denote the current in this wire.
The magnetic force on the wire would be:
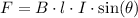 .
.
Because of the
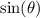 term, the magnetic force on the wire is maximized when the wire is perpendicular to the magnetic field (such that the angle between them is
term, the magnetic force on the wire is maximized when the wire is perpendicular to the magnetic field (such that the angle between them is
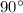 .)
.)
In this question:
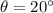 (or, equivalently,
(or, equivalently,
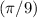 radians, if the calculator is in radian mode.)
radians, if the calculator is in radian mode.)
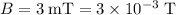 .
.
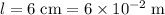 .
.
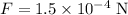 .
.
Rearrange the equation
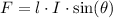 to find an expression for
to find an expression for
 , the current in this wire.
, the current in this wire.
 .
.