1 Answer

Petro · Answer 1 · 2022-08-09T19:23:27+0000

Given:

The expressions are

(c)
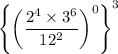
$\left\{\left((2^4* 3^6)/(12^2)\right)^0\right\}^3$

(d)
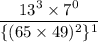
$\frac{13^3* 7^0}{\{(65* 49)^2\}^1}$

To find:

The simplified form of the given expression.

Solution:

(c)

We have,

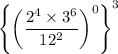
$\left\{\left((2^4* 3^6)/(12^2)\right)^0\right\}^3$

We know that, zero to the power of a non-zero number is always 1. So,
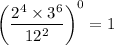
$\left((2^4* 3^6)/(12^2)\right)^0=1$

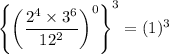
$\left\{\left((2^4* 3^6)/(12^2)\right)^0\right\}^3=(1)^3$

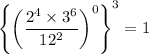
$\left\{\left((2^4* 3^6)/(12^2)\right)^0\right\}^3=1$

Therefore, the value of the given expression is 1.

(d)

We have,

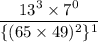
$\frac{13^3* 7^0}{\{(65* 49)^2\}^1}$

It can be written as

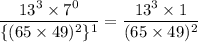
$\frac{13^3* 7^0}{\{(65* 49)^2\}^1}=(13^3* 1)/((65* 49)^2)$

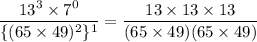
$\frac{13^3* 7^0}{\{(65* 49)^2\}^1}=(13* 13* 13)/((65* 49)(65* 49))$

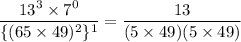
$\frac{13^3* 7^0}{\{(65* 49)^2\}^1}=(13)/((5* 49)(5* 49))$

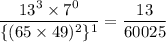
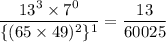
$\frac{13^3* 7^0}{\{(65* 49)^2\}^1}=(13)/(60025)$

Therefore, the value of given expression is
.

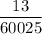Please log in or register to add a comment.