Given:
x is directly proportional to y and inversely proportional to z.
x= 15 when y = 10 and z= 4.
To find:
The equation that connecting x, y and z.
Solution:
It is given that, x is directly proportional to y and inversely proportional to z.
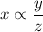
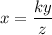 ...(i)
...(i)
Where, k is the constant of proportionality.
We have, x= 15 when y = 10 and z= 4.
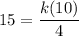
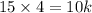
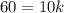
Divide both sides by 10.
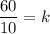
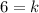
Putting k=6 in (i), we get
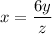
Therefore, the required equation is
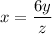 .
.