Question

A consulting firm has bid on two projects, A and B. The probability of landing A is 0.70. The probability of landing B is 0.60. The probability of landing both is 0.50.

What is the probability of landing A given it lands B?

Answer 1

Given:

The probability of landing A is 0.70.

The probability of landing B is 0.60.

The probability of landing both is 0.50.

To find:

The probability of landing A given it lands B.

Solution:

We have,

`P(A) = 0.70`

`P(B) = 0.60`

`P(A\cap B) = 0.50`

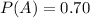
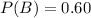
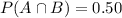
The probability of landing A given it lands B is

`P\left((A)/(B)\right)=(P(A\cap B))/(P(B))`

`P\left((A)/(B)\right)=(0.50)/(0.60)`

`P\left((A)/(B)\right)=(5)/(6)`

`P\left((A)/(B)\right)=0.8333...`

`P\left((A)/(B)\right)\approx 0.83`

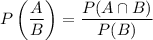
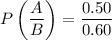
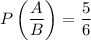
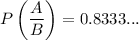
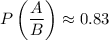
Therefore, the probability of landing A given it lands B is about 0.83.