Answer:
The absolute minimum of the function
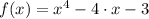 occurs at
occurs at
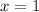 and is
and is
 .
.
Step-by-step explanation:
Statement is incorrect. Correct statement is presented below:
Given the function
 , determine the absolute minimum value of
, determine the absolute minimum value of
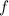 on the closed interval
on the closed interval
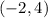 . First, we determine the first and second derivatives of the function.
. First, we determine the first and second derivatives of the function.
First Derivative
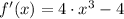 (1)
(1)
Second Derivative
 (2)
(2)
By equalizing (1) to zero, we solve for
 :
:
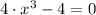
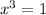
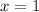
And we evaluated this result in (2):

According to criteria of the Second Derivative Test, we conclude that value of
 leads to an absolute minimum. The value of the absolute minimum is:
leads to an absolute minimum. The value of the absolute minimum is:

The absolute minimum of the function
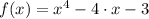 occurs at
occurs at
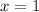 and is
and is
 .
.