Geometric Solids: Prism
For a prism we take into account the following:
Taking into account the above, we first find the lateral area:
In the triangular base, the height divided into 2 small right triangles of Hypotenuse = 5 and Height = 3. By Pythagoras we have this:
3² + base² = 5²
9 + base² = 25
base² = 25 - 9
base² = 16
base = 4
From this we obtain that the bases of the small right triangles measure 4 therefore the triangular base is isosceles where we have:
The perimeter of the triangular base will be the sum of the sides, that is:
Perimeter = 5 + 5 + 8
⇒ Perimeter = 18
Since the perimeter of the base of the prism is 18 and the height is 20, we replace in the equation for the lateral area:
Side area = (18) (20)
⇒ Lateral Area = 360 m²
Now we find the area of the triangular base with base = 8 and height = 3:
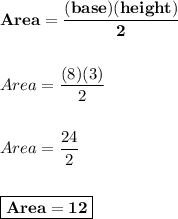
Since we have that the lateral area is 360m² and the area of the triangular base is 12m², we replace in the equation of the total area:
Total area = 360 + 2 (12)
Total area = 360 + 24
Total area = 384 m²
The total area of the prism will measure 384m²
I hope I have helped you, greetings from Venezuela!