Answer:
25° and 97°
Explanation:
Oblique triangle : any triangle that is not a right triangle
Use the sine rule to find one of the unknown interior angles:
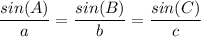
where A, B and C are the interior angles of a triangle, and a, b and c are the sides opposite to the interior angles.

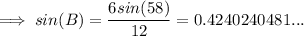

Sum of interior angles of a triangle = 180°
⇒ Missing angle = 180 - 58 - 25 = 97°