Question

A coin dropped in the lift it takes time 0.5 s to reach the floor when lift is staionary it takes time t when lift is moving up

Answer 1

t₁ > t₂

Step-by-step explanation:

A coin is dropped in a lift. It takes time t₁ to reach the floor when lift is stationary. It takes time t₂ when lift is moving up with constant acceleration. Then t₁ > t₂, t₁ = t₂, t₁ >> t₂ , t₂ > t₁

Solution:

Newton's law of motion is given by:

s = ut + (1/2)gt²;

where s is the the distance covered, u is initial velocity, g is the acceleration due to gravity and t is the time taken.

u = 0 m/s, t₁ is the time to reach ground when the light is stationary and t₂ is the time to reach ground when the lift is moving with a constant acceleration a.

hence:

When stationary:

`s=(1)/(2)gt_1^2\\\\t_1^2=(2s)/(g) \\\\When\ moving\ with\ acceleration(a):\\\\s=(1)/(2)(g+a)t_2^2\\\\t_2^2=(2s)/(g+a)`

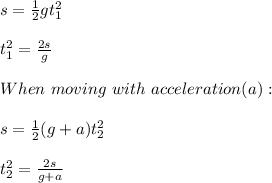
Hence t₂ < t₁, this means that t₁ > t₂.