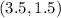Answer:

Explanation:
The midpoint is essentially a point with the average of the 2 x-coordinates and the 2 y-coordinates.
The formula is:
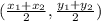
We are given two points: A (7,0) and B (0, 3). Remember points are written as (x, y).
Therefore,
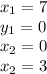
Substitute the values into the formula.
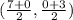
Solve the numerators first.
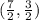
The midpoint can be left like this because the fractions are reduced, but it can be written as decimals too.