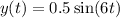Solution :
Given :
Weight = 4 lb
Stretched of a spring in equilibrium,Δ = 2 ft
a). We know that
F = kΔ
4 = k x 2
k = 2 lb/ft
∴ Stiffness of the spring is, k = 2 lb/ft
Motion is critically damped.
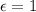


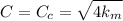

C = 0.99729 lb.s/ft.
b). Displacement

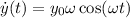
![$[\dot{y}(t)]_(mon)= y_0 \omega $](https://img.qammunity.org/2022/formulas/physics/college/fs8la73xcgcyk05y3kk57ymcbdiuhr107w.png)
Initial displacement = 6 inches
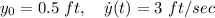

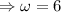
Therefore, displacement :