Answer:
x - 1
Explanation:
Identity used: (a² - b²) = (a + b)(a - b)
Given:
f(x) = x² - 1
g(x) = x + 1
Finding f(x) / g(x):
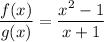
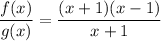 (using the property mentioned)
(using the property mentioned)
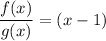 (cancelling (x + 1) from the numerator and denominator)
(cancelling (x + 1) from the numerator and denominator)
Hence, f(x) / g(x) = (x - 1)
(where x doesn't equal -1)