Question

If Y is the circumcenter of
Please help I’m
Failing

Answer 1

Measures are SV=9 units., SY=14 units, YW=
`√(75units)`, YW=
`√(27units)`

Step-by-step explanation:

Answer 2

Answer: 8.7 (choice B)

===================================================

Step-by-step explanation:

The circumcenter is found by intersecting the perpendicular bisectors of the triangle.

Segments VY, WY, and XY are perpendicular bisectors of triangle STU.

A perpendicular bisector has two properties:

1. It is perpendicular to the given side, i.e. it forms a 90 degree angle.
2. It divides the segment into two equal pieces.

Perpendicular bisector WY divides side TU into equal pieces TW and WU

In short:

TW = WU

So

TW = 11

since WU is equal to 11 as well

---------------------------------------

Focus on triangle TWY.

This is a right triangle with the sides of...

• TW = 11 = one leg
• YW = unknown = the other leg
• YT = 14 = hypotenuse

We'll use the pythagorean theorem to determine the unknown leg.

Plug in a = 11 and c = 14. Then let's solve for b.

`a^2+b^2 = c^2\\\\11^2+b^2 = 14^2\\\\121+b^2 = 196\\\\b^2 = 196-121\\\\b^2 = 75\\\\b = √(75)\\\\b \approx 8.66025\\\\b \approx 8.7\\\\`

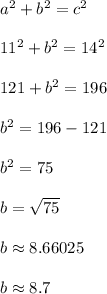
Therefore, segment YW is roughly 8.7 units.