Question

When a 2.00-kg object is hung vertically on a certain light spring described by Hooke's law, the spring stretches 2.88 cm and stays at that position without moving. The force of gravity downward balances the spring force upward. (a) What is the force constant of the spring? (b) If the 2.00-kg object is removed, how far will the spring stretch if a 1.00-kg block is hung on it? (c) How much work must an external agent do to stretch the same spring 9.00 cm from its unstretched position?

Answer 1

The spring constant is approximately
`681\; {\rm N \cdot m^(-1)}`.

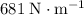The spring would stretch approximately
`1.44\; {\rm cm}`.

Approximately
`2.76\; {\rm J}` of energy is required to stretch this spring to the required position.

(Assumption:
`g = 9.81\; {\rm m\cdot s^(-2)}`.)

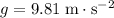Step-by-step explanation:

Make sure all displacements are measured in standard units:

`2.88\; {\rm cm} = 0.0288\; {\rm m}`.

`9.00\; {\rm cm} = 0.0900\; {\rm m}`.

(a)

To find the spring constant
`k`, divide force on the spring
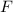`F` by displacement
`x`. That is:
`k = F / x`.

In this question, force on the spring is equal to the weight of the object. To find the weight of the object, multiply mass
`m` by
`g`:

`\begin{aligned}(\text{weight}) &= m\, g \\ &= (2.00\; {\rm kg}) \, (9.81\; {\rm N\cdot kg^(-1)}) \\ &= 19.62\; {\rm N}\end{aligned}`.

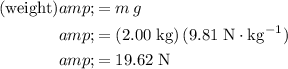Substitute
`F = (\text{weight}) = 19.62\; {\rm N}` into the equation
`k = F / x` to find the spring constant
`k`:

`\begin{aligned} k &= (F)/(x) \\ &= \frac{19.62\; {\rm N}}{0.0288\; {\rm m}} = 681.25\; {\rm N\cdot m^(-1)}\end{aligned}`.

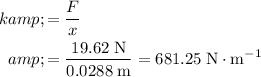(b)

By Hooke's Law, as long as spring constant
`k` is fixed, displacement of the spring would be proportional to the external force on the spring.

If
`g` is fixed, the weight of an object will be proportional to its mass. Hence, the weight of the
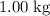`1.00\; {\rm kg}` object would be
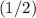`(1/2)` that of the
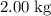`2.00\; {\rm kg}` object.

Therefore, reducing the mass of the object on the spring by
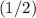`(1/2)` would also reduce the displacement of the spring by
`(1/2)\!`.

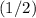(c)

If the spring constant
`k` is fixed, the work required to stretch the spring by
`x` is given by the formula
`(1/2)\, k\, x^(2)`.

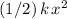In this example, it is already found that
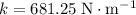`k = 681.25\; {\rm N \cdot m^(-1)}`. The energy required to stretch the spring by
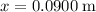`x = 0.0900\; {\rm m}` would be:

`\begin{aligned} (1)/(2)\, k\, x^(2) =\; & (1)/(2)\, (681.25\; {\rm N \cdot m^(-1)})\, (0.0900\; {\rm m})^(2) \\ \approx \; & 2.76\; {\rm J}\end{aligned}`.