Rational Function: any function that is found by a rational fraction.
Its form:
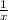
Finding Zeros of a Rational Function:
- Factor Numerator and denominator
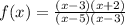
2. Find restrictions by equating the denominator to 0
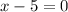
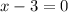 when x=-5 and 3, the function is undefined
when x=-5 and 3, the function is undefined

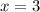
3. Set the numerator equal to zero
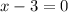
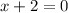
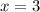

Be careful - since we have x-3 on both the numerator and denominator the graph will not intersect the x-axis at that point. This is what is called a removable discontinuity.
Therefore, the only zero occurs at (-2,0)