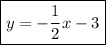Answer:
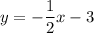
Explanation:

Given equation:
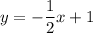
Parallel lines have the same slope.
Therefore, the slope of the line parallel to the given equation is:
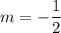
Substitute the found slope and given point (-4, -1) into the point-slope formula:
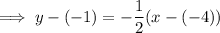
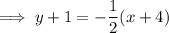
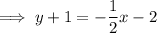
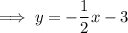
Therefore, the equation of the line passing through (-4, -1) and parallel to the given equation is: