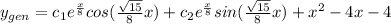Answer:

Explanation:
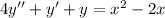
First, we find the homogenous solution to this differential equation by solving
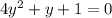 and we will get
and we will get
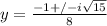 .
.
Recall that the homogenous solution, when roots are in complex form (
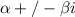 ), is
), is
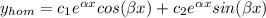 when
when
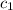 and
and
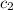 are undetermined coefficients. So substituting
are undetermined coefficients. So substituting
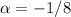 and
and
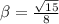 , we would get the equation
, we would get the equation
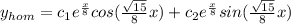
However, we are not done. We still have to find the particular solution to this inhomogenous equation by using undetermined coeffeicients. This means we are going to take the term g(x), or the term containing no y terms, and find a match to substitute it.
In this case, it is a polynomial, so the substitute must be a polynomial of the same degree. We'll say it is
 . If
. If
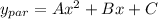 , that means
, that means
 and
and
 . Substitute the three into the differential equation, we get
. Substitute the three into the differential equation, we get
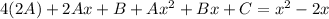
From here we can solve for
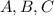 which is 1, -4, -4. And we can just substitute that into out particular solution to get
which is 1, -4, -4. And we can just substitute that into out particular solution to get
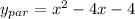 . Combining the homogenous solution and the particular solution, we get that the general solution is
. Combining the homogenous solution and the particular solution, we get that the general solution is