Answer:
Explanation:
You want to know various values of p and q when p varies inversely as the square of q, and p=36 when q=25.
Variation
A formula describing the variation of one variable with another will generally have a constant of variation, which we choose to represent here by the letter k.
Since p varies inversely as the square of q, the formula can be written as ...
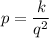
Multiplying by q² gives us a way to find the value of k from known values of p and q:
k = p·q²
k = 36·25² = 22500 . . . . . . using the given values of p and q
We can also rearrange the formula to give q as a function of p:
q = √(k/p)
Table of values
We are interested in q for p=4, and in p for q=10.
q = √(22500/4) = 75
p = 22500/10² = 225
- When p=4, q = 75
- When q=10, p = 225