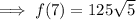Question

If f(x) = r to the power x where r > 0 and if f(6) = 125, what is the value of f(7) ?

help fpr gods sake

Answer 1

`f(7)=125√(5)`

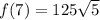
Explanation:

Given function:

`f(x)=r^x, \quad r > 0`

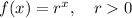
If f(6) = 125, substitute x = 6 into the function and equate it to 125:

`\implies r^6=125`

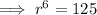
Rewrite 125 as 5³:

`\implies r^6=5^3`

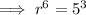
Cube root both sides of the equation:

`\implies \sqrt[3]{r^6}=\sqrt[3]{5^3}`

`\textsf{Apply exponent rule} \quad \sqrt[n]{a^b}=a^{(b)/(n)}:`

`\implies r^{(6)/(3)}=5^{(3)/(3)}`

`\implies r^(2)=5^1`

`\implies r^(2)=5`

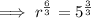
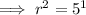
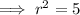
Square root both sides of the equation:

`\implies √(r^2)=√(5)`

`\implies r=\pm √(5)`

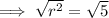
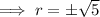
As r > 0 then r = √5

Therefore the function is:

`f(x)=\left(√(5) \right)^x`

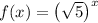
To calculate f(7), substitute x = 7 into the found function:

`\implies f(7)=\left(√(5) \right)^7`

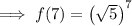
`\textsf{Apply exponent rule} \quad \sqrt[n]{a}=a^{(1)/(n)}:`

`\implies f(7)=(5^{(1)/(2)})^7`

`\textsf{Apply exponent rule} \quad (a^b)^c=a^(bc):`

`\implies f(7)=5^{(7)/(2)}`

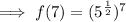
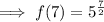
Rewrite ⁷/₂ as 3 + ¹/₂ :

`\implies f(7)=5^{\left(3+(1)/(2)\right)}`

`\textsf{Apply exponent rule} \quad a^(b+c)=a^b \cdot a^c:`

`\implies f(7)=5^3 \cdot 5^{(1)/(2)}`

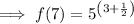
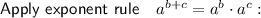
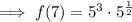
Simplify:

`\implies f(7)=125 √(5)`