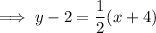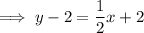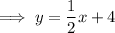Question

Does someone mind helping me with this problem? Thank you!

Answer 1

`y=\frac{\boxed{1}}{\boxed{2}}\:x+\boxed{4}`

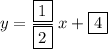
Explanation:

`\boxed{\begin{minipage}{6.3 cm}\underline{Slope-intercept form of a linear equation}\\\\$y=mx+b$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $b$ is the $y$-intercept.\\\end{minipage}}`

Therefore, the slope of the given line y = -2x + 5 is -2.

If two lines are perpendicular to each other, their slopes are negative reciprocals.

Therefore, the slope of a perpendicular line ¹/₂.

`\boxed{\begin{minipage}{5.8 cm}\underline{Point-slope form of a linear equation}\\\\$y-y_1=m(x-x_1)$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $(x_1,y_1)$ is a point on the line.\\\end{minipage}}`

Substitute the found slope and point (-4, 2) into the point-slope formula:

`\implies y-2=(1)/(2)(x-(-4))`

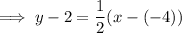
Rearrange to slope-intercept form:

`\implies y-2=(1)/(2)(x+4)`

`\implies y-2=(1)/(2)x+2`

`\implies y=(1)/(2)x+4`