Question

Find the equation of a line perpendicular to\hspace{4px}-x+y=9\hspace{4px}−x+y=9that passes through the point (-2,-1)(−2,−1).

Answer 1

`y = -x -3`

Explanation:

⭐What is a property of a perpendicular line?

• perpendicular lines have slopes that are the opposite reciprocal of the slopes of the lines they are perpendicular to

⭐What does "opposite reciprocal" mean?

• the perpendicular line has a slope that is the reciprocal of the slope of the line it is perpendicular to with the opposite sign.

⭐What is the equation of a line?

• in slope-intercept form:
• 
  `y = mx + b`
• m = the slope
• b = the y-intercept

To create the equation of the perpendicular line, let's first find the slope of the perpendicular line.

The equation of the line the perpendicular line is perpendicular to is:

`-x + y = 9`

⭐
`y = x + 9`

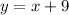
The slope of the line the perpendicular line is perpendicular to is 1.

Therefore, the slope of the perpendicular line is -1.

Substitute the slope of the perpendicular line into the equation of the perpendicular line:

`y = mx + b`

`y = -x + b`

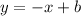
Now, we need to find the y-intercept of the perpendicular line.

To do so, substitute a point that we are given into the perpendicular line equation and solve for b.

I am going to use the point (-2,-1), because we are given this point.

`y = -x + b`

`-1 = -(-2) + b`

`-1 = 2 + b`

`-3 = b`

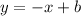
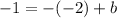
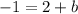
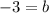
Therefore, the y-intercept of the perpendicular line is -3.

Substitute the value of the y-intercept into the equation of the perpendicular line:

`y = -x -3`

∴The equation of the perpendicular line is
`y = -x -3`