Question

Solve the equation


`3 \csc ^(2) (x) = 5 - 5 \cot(x)`
, given all values of x in the interval

`- \pi \leqslant x \leqslant \pi`
​

Answer 1

To solve the equation
`3 \csc ^(2) (x) = 5 - 5 \cot(x)`, we will start by rewriting the right-hand side of the equation using the identity
`\cot x = (1)/(\tan x)`:

`3 \csc ^(2) (x) = 5 - 5 (1)/(\tan(x))`

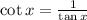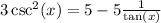
Next, we will use the identity
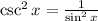`\csc^2 x = (1)/(\sin^2 x)` to rewrite the left-hand side of the equation:

`(3)/(\sin ^(2) (x)) = 5 - 5 (1)/(\tan(x))`

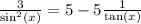
Now, we will use the identity
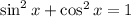`\sin^2 x + \cos^2 x = 1` to rewrite the denominator on the left-hand side:

`(3)/(1 - \cos^2 x) = 5 - 5 (1)/(\tan(x))`

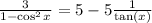
Next, we will use the identity
`\tan^2 x = \sec^2 x - 1` to rewrite the fraction on the right-hand side:

`(3)/(1 - \cos^2 x) = 5 - 5 (\sec^2 x - 1)`

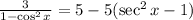
Now, we will distribute the negative sign on the right-hand side:

`(3)/(1 - \cos^2 x) = 5 - 5 \sec^2 x + 5`

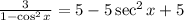
Combining like terms on the right-hand side gives us:

`(3)/(1 - \cos^2 x) = 10 - 5 \sec^2 x`

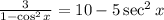
Adding 5 to both sides and then dividing both sides by 10 gives us:

`(3 + 5)/(10) = 1 - (5)/(10) \sec^2 x`

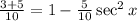
Simplifying the left-hand side gives us:

`(8)/(10) = 1 - (5)/(10) \sec^2 x`

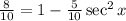
Multiplying both sides by 10 and rearranging terms gives us:

`\sec^2 x = (10 - 8)/(5) = (2)/(5)`

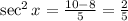
Taking the square root of both sides gives us:

`\sec x = \pm (√(2))/(√(5))`

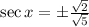
To find the values of x that satisfy the equation, we need to find the values of x in the interval
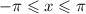`-\pi \leqslant x \leqslant \pi` that give us a positive value for
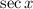`\sec x`. Since the secant function is positive for all values of x in the interval
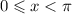`0 \leqslant x < \pi`, all values of x in this interval will satisfy the equation.

Therefore, the solution to the equation is
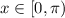`x \in \left[ 0, \pi \right)`.