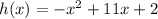Answer:
Explanation:
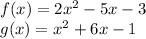
As the question is saying
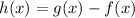 , we need to substitute the values of
, we need to substitute the values of
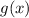 and
and
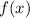 into this equation to solve for
into this equation to solve for
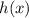 .
.
Substitute the values of g(x) and f(x) into the h(x) equation:
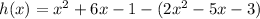
Distribute the negative sign into the expression for f(x):
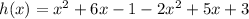
Add the like terms (terms with the same variable and same exponent) to simplify:
⭐
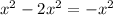
⭐
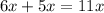
⭐
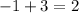
∴