Question

A ladybug is moving at a speed of one centimeter per second. She begins to decelerate at a

rate of -0. 25 centimeters per second squared until she comes to rest. How much distance does

the ladybug cover from the moment she begins to decelerate until the moment she comes to

rest?

Answer 1

2 meters

Step-by-step explanation:

What we know from the problem are:

1. initial speed (u) = 1 cm/s
2. acceleration (a) = - 0.25 cm/s²
3. final speed (v) = 0 m/s (Moving til rest)

From the acceleration formula:

`\displaystyle{ a = (v - u)/(t)}`

Substitute in:

`\displaystyle{ - 0.25 \ \text{m/s}^(2) = \frac{ - 1 \ \text{m/s}}{t}} \\ \\ \displaystyle{ - 0.25 \ \text{m/s}^(2) \ \cdot t = - 1 \ \text{m/s}} \\ \\ \displaystyle{ t = \frac{ - 1 \ \text{m/s}}{ - 0.25 \ \text{m/s}^(2) }} \\ \\ \displaystyle{ t = 4 \ \text{s}}`

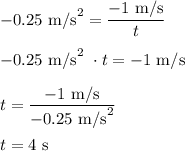
Now we know that at 4 seconds, the ladybug is at rest. Therefore, from the distance formula:

`\displaystyle{s = ut + (1)/(2)a {t}^(2) }`

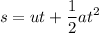
Substitute in:

`\displaystyle{s = (1)(4) + (1)/(2)( - 0.25) {(4)}^(2) } \\ \\ \displaystyle{s = 4+ (1)/(2)( - 0.25) (16) } \\ \\ \displaystyle{s = 4 - 0.25 \cdot 8} \\ \\ \displaystyle{s = 4 - 2} \\ \\ \displaystyle{s = 2 \ \text{meters}}`

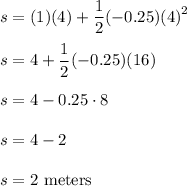
Therefore, she will cover distance of 2 meters.