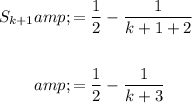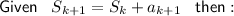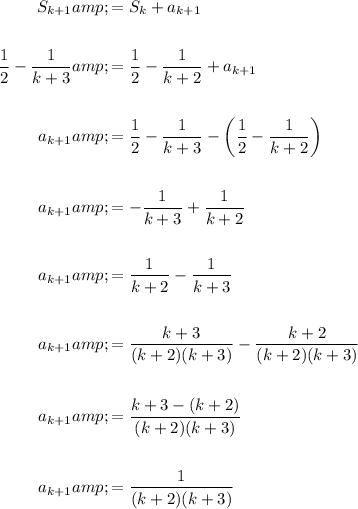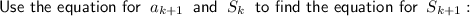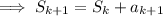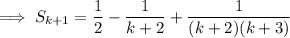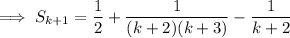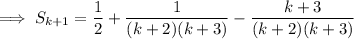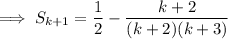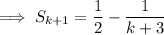Answer:
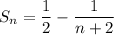
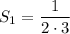
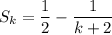
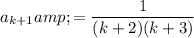
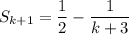
Explanation:
Given sequence:
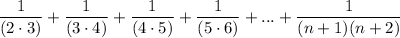
Rewrite the numerator as the subtraction of the first number of the denominator from the second number of the denominator:
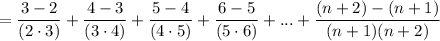
Simplify:
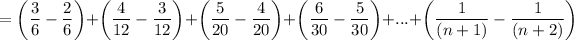
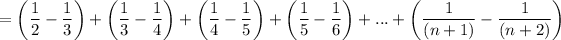
All fractions cancel except the first and last.
Therefore the formula for the sum of the given sequence is:
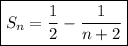
Substitute n = 1 into the formula to prove its validity:
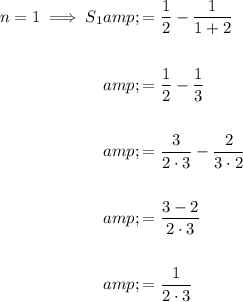
Hence proving the validity of the formula.
Assume the formula is valid for n = k :
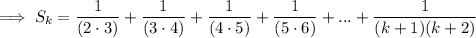
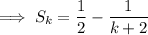
Therefore: