Question

NO LINKS!!

Use a graphing utility to graph the function to approximate (to 2 decimal places) any relative minima or maxima of the function. (If the answer does not exist, enter DNE)
h(x) = x^3 - 6x^2 + 15

relative minimum (x, y) = (______)
relative maximum (x, y)= (______)

Answer 1

Relative minimum (x, y) = (4, -17)

Relative maximum (x, y) = (0, 15)

Explanation:

Given function:

`h(x) = x^3 - 6x^2 + 15`

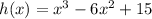
Use a graphing calculator to graph the function (see attachment).

The relative minima and maxima of a function are the turning points.

From inspection of the graphed function:

• Relative minimum (x, y) = (4, -17)
• Relative maximum (x, y) = (0, 15)

To find the x-values of the turning points, differentiate the function:

`\implies h'(x)=3x^2-12x`

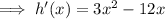
Then set the derivative of the function to zero and solve for x:

`\implies 3x^2-12x=0`

`\implies 3x(x-4)=0`

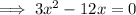
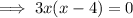
Therefore the x-values of the turning points are:

• x = 0
• x = 4

To find the y-values, substitute the x-values into the function:

`\implies h(0)=(0)^3-6(0)^2+15=15`

`\implies h(4)=(4)^3-6(4)^2+15=-17`

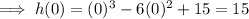
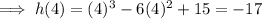
Therefore, this confirms that the maxima and minima are:

• (0, 15) and (4, -17)

Answer 2

Given function:

• h(x) = x³ - 6x² + 15

This is an odd degree function with positive leading coefficient. It means the graph is increasing and may have two turning points which are called local minimum/maximum or relative minimum/maximum.

As per graph it has:

• Relative minimum at (4, - 17) and
• Relative maximum at (0, 15).

The graph is attached.