Answer:
3
Explanation:
The given points indicate that the triple integral should be from 0-1 in the x-direction, 0-2 in the y-direction, and 0-3 in the z-direction. So,
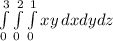
This triple integral can be broken into three steps. Evaluate the innermost integral with respect to x:
![\int\limits^1_0 {xy} \, dx\\(1)/(2)x^2y]_0^1\\(1)/(2)[(1)^2y]-(1)/(2)[(0)^2y]\\(1)/(2)y](https://img.qammunity.org/2023/formulas/mathematics/college/9w2po1ccnnl86hohtzhmx7f4pe7oqrxctz.png)
Next, use
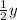 to evaluate the middle integral with respect to y:
to evaluate the middle integral with respect to y:
![\int\limits^2_0 {(1)/(2)y} \, dy\\(1)/(2)\int\limits^2_0 {y} \, dy\\(1)/(2)((1)/(2)y^2)]_0^2\\(1)/(4)[(2)^2-(0)^2]\\(1)/(4)(4)\\1](https://img.qammunity.org/2023/formulas/mathematics/college/644t0mtyub53eykezl67nko1gks6zbr4ap.png)
Finally, use 1 to evaluate the outermost integral with respect to z:
![\int\limits^3_0 {1} \, dz\\z]_0^3\\(3)-(0)\\3](https://img.qammunity.org/2023/formulas/mathematics/college/sncgrin77iuu0hye0lrkyuvnzrvr8hu780.png)
So, the final value of the triple integral is 3